Answer: B
Solution:
Since Brianna is half of Aunt Anna's age this means that Brianna is 21 years old. Now we just find Caitlin's age by doing 21-5=16.
Answer: A
Solution:
The number 0 has no reciprocal, the reciprocal of 1 is 1, the reciprocal of -1 is -1. This leaves only 2 ,-2. The reciprocal of 2 is 1/2, but 2 is not less than 1/2. The reciprocal of -2 is -1/2, -2 is less than-1/2, so it is A.

Answer: D
Solution:
The smallest whole number in the interval is 2 because 5/3 is more than 1 but less than 2. The largest whole number in the interval is 6 because 2Pi is more than 6 but less than 7. There are five whole numbers in the interval. They are 2,3,4,5,6, so the answer is D.
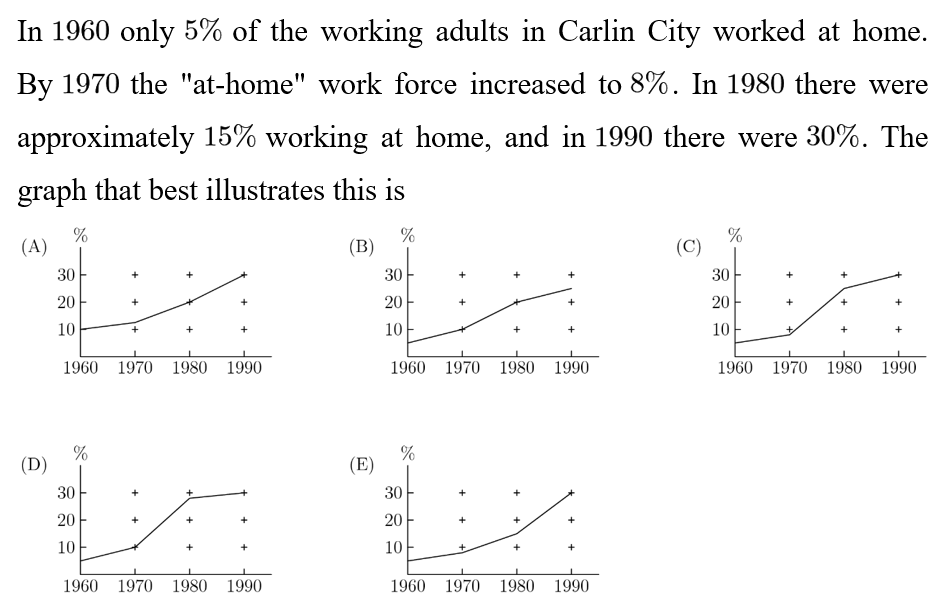
Answer: E
Solution:
The data are 1990(5%), 1970(8%), 1980(15%),and 1990(30%). Only one of these graphs has the answer and that is choice E.

Answer: C
Solution:
If the first year of the 8-year period was the final year of a principal's term, then in the next six years two more principals would serve, and the last year of the period would be the first year of the fourth principal's term. Therefore, the maximum number of principals who can serve during an 8-year period is 4.

Answer: A
Solution:
Solution: A (area)
The shaded area can be divided into three regions: one small square with side 1, and two rectangles with a length and width of 1 and 3. The sum of these three areas is 1*1+3*1+1*3=7.

Answer: B
Solution:
The only way to get a negative product using three numbers is to multiply one negative number and two positives or three negatives. Only two reasonable choices exist: (-8)*(-6)*(-4)=-192 ; (-8)*5*7=-280. The latter is smaller, so the answer is 280.

Answer: D
Solution:
The numbers on one die total 1+2+3+4+5+6=21, so the numbers on the three dice total 63. Numbers 1,1,2,3,4,5,6 are visible, and these total 22. This leaves 63-22=41 not seen.

Answer: D
Solution:
The 3-digit powers of 5 are 125 and 625, so space 2 is filled with a 2. The only 3-digit power of 2 beginning with 2 is 256, so the outlined block is filled with a 6.

Answer: E
Solution:
Shea has grown 20%, if x was her original height, then 1.2x=60, so she was originally 60/1.2=50 inches tall which is a 60-50=10 inch increase. Ara also started off at 50 inches. Since Ara grew half as much as Shea, Ara grew 10/2=5 inches. Therefore, Ara is now 50+5=55 inches tall.

Answer: C
Solution:
U=0 gives no solutions, since no real numbers are divisible by 0;
U=1 has 4 solutions, since all numbers are divisible by 1;
U=2 has 4 solutions, since every number ending in 2 is even;
U=3 has 1 solution:33;
U=4 has 2 solutions: 24 and 44;
U=5 has 4 solutions: every number ending in 5 is divisible by 5;
U=6 has 1 solution: 36;
U=7 has no solutions;
U=8 has 1 solution: 48
U=9 has no solutions.
Totally we have 0+4+4+1+2+4+1+0+1+0=17 solutions.
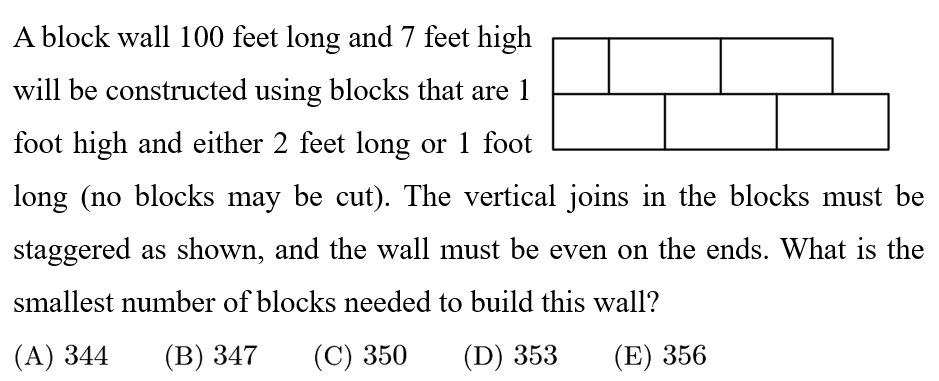
Answer: D
Solution:
Since the bricks are 1 foot high, there will be 7 rows. To minimize the number of blocks used, rows 1,3,5 and 7 will look like the bottom row of the picture, which takes 100/2=50 bricks to construct. Rows 2,4 and 6 will look like the upper row pictured, which has 49 2-foot bricks in the middle, and 2 1-foot bricks on each end for a total of 51 bricks. Four rows of 50 bricks and three rows of 51 bricks totals 4*50+3*51=353 bricks.

Answer: C
Solution:
In triangle ACT, <c=<T=(180-36)/2=72. <RTC=1/2*<ATC=36;
In Triangle CRT, <c=72, <RTC=36, thus <CRT=180-72-26=72.
Answer: D
Solution:
even powers of 19 have a units digit of 1, and odd powers of 19 have a units digit of 9. So, 19^19 has a units digit of 9. Powers of 99 have the exact same property, so 99^99 also has a units digit of 9. 9+9=18 which has a units digit of 8.
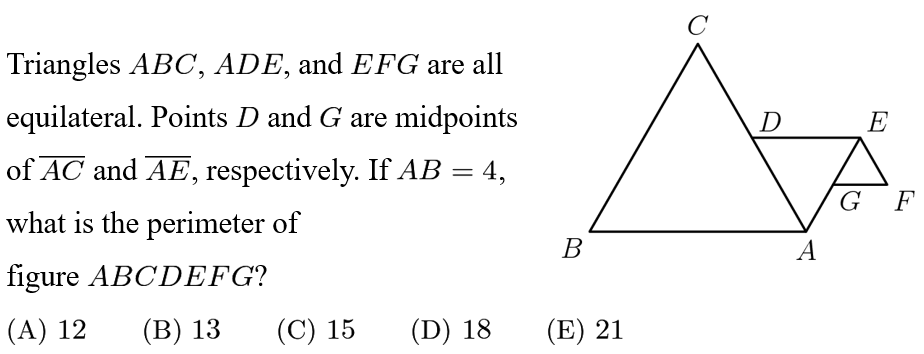
Answer: C
Solution:
The large triangle ABC has sides of length 4. The medium triangle has sides of length 2. The small triangle has sides of length 1. There are 3 segment sizes, and all segments depicted are one of these lengths.
Starting at A and going clockwise, the perimeter is:
AB+BC+CD+DE+EF+FG+GA=4+4+2+2+1+1+1=15.

Answer: C
Solution:
The length L of the rectangle is 1000/25=40 meters. The perimeter is 1000/10=100 meters. So the width is 100/2-40=10 meters. Area is 40*10=400 .

Answer: A
Solution:
1@2=1*1/2=1/2; 1/2@3=(1/4)/3=1/12;
2@3=4/3;1@4/3=1/(4/3)=3/4;the answer is 1/12-3/4=-2/3.

Answer: E
Solution:
Area of quadrilateral I is : 1/2*1*1+1/2*1*1=1;
Area of quadrilateral II is : 1/2*1*1+1/2*1*1=1;
Perimeter of quadrilateral I is : 1+sqrt(2)+1+sqrt(1);
Perimeter of quadrilateral II is : sqrt(5)+sqrt(2)+1+sqrt(2)

Answer: C
Solution:
Draw line BD. Then draw CO, where o is the center of the semicircle. You have two quarter circles on top, and two quarter circle-sized "bites" on the bottom. Move the pieces from the top to fit in the bottom like a jigsaw puzzle. You now have a rectangle with length BD and height AO, which are equal to 10 and 5, respectively. Thus, the total area is 50.

Answer: A
Solution:

Answer: B
Solution:
Let K(n) be the probability that Keiko gets n heads, and let E(n) be the probability that Ephriam gets n heads. E(0)=1/4; E(1)=1/2; E(2)=1/4; K(0)=1/2; K(1)=1/2; K(2)=0;
The probability that Keiko gets 0 heads and Ephriam gets 0 heads is K(0)*E(0)=1/2*1/4=1/8; Similarly for 1 head and 2 heads. Thus, we have:P=K(0)*E(0)+K(1)*E(1)+K(2)*E(2)=1/8+1/2*1/2+0=3/8.

Answer: C
Solution:
The original cube has 6 faces, each with an area of 2*2=4 square units. Thus the original figure had a total surface area of 24 square units.
The new figure has the original surface, with 6 new faces that each have an area of 1 square unit, for a total surface area of 6 additional square units added to it. But 1 square unit of the top of the bigger cube, and 1 square unit on the bottom of smaller cube, is not on the surface, and does not count towards the surface area.
The total surface area is therefore 24+6-1-1=28 square units.
The percent increase in surface area 28-24/24=4/24=17%

Answer: B
Solution:
Let the sum of first 3 numbers is a, the fourth number is x, and the sum of last 3 numbers is c, then :
a+x=5*4;
x+b=8*4;
a+x+b=7*(46/7);
we get x=6 from the above 3 equations.
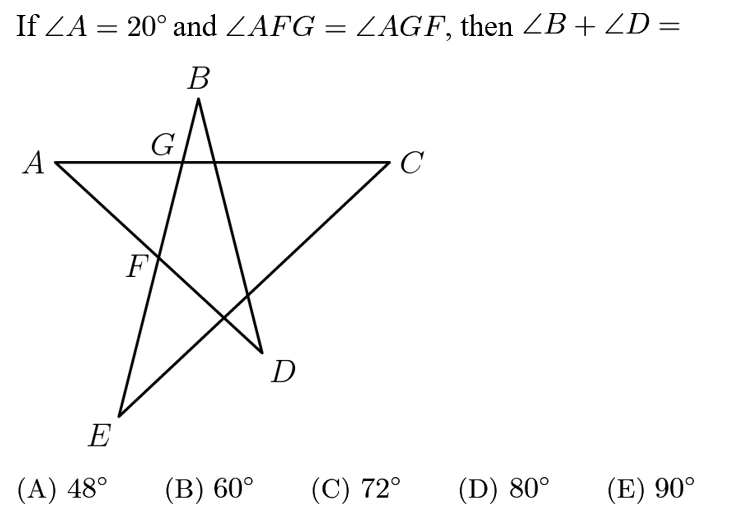
Answer: D
Solution:
<AFG=(180-<A)/2=80;thus , <BFD=180-<AFG=100;
In Triangle BFD; <B+<D=180-<BFD=180-100=80.
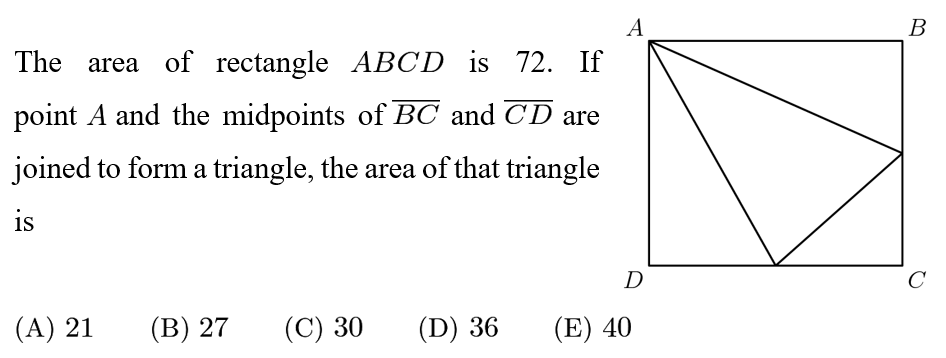
Answer: B
Solution:
To quickly solve this multiple choice problem, make the (not necessarily valid, but very convenient) assumption that ABCD can have any dimension. Give the rectangle dimensions of AB=CD=12 and BC=AD=6, which is the easiest way to avoid fractions. Labelling the right midpoint as M, and the bottom midpoint as N, we know that DN=NC=6; BM=MC=3.
Area(AND)=1/2*6*6=18; Area(MNC)=1/2*6*3=9; Area(ABM)=1/2*12*3=18; Area(AMN)=Area(ABCD)-Area(AND)-Area(MNC)-Area(ABM)=72-18-9-18=27.
AMC培训、答疑,请联系微信 / 电话:136 1118 1627
艾蕾特教育 @Elite Edu, 在这里,